Fast Fourier Transform (FFT) algorithms typically operate by recursively (though perhaps not literally using recursion in the code) breaking down the input into prime-factor-length sub-problems. Thus, the overall speed of the funciton depends on the largest prime factor, and prime inputs may be slow because they can't be broken down at all.
But how much slower are these prime inputs? If they're much slower, we may want to pad the input with zeros. This is generally okay, but depending on your input may cause window-related artifacts in your output.
Here's a quick benchmark of a 1D complex FFT using scipy.fft (which I believe
uses pocketFFT). This shows the
minimum execution time of 10 runs for random (uniform) complex data up to input
length 2**16. Prime inputs are highlighted by the red dots.
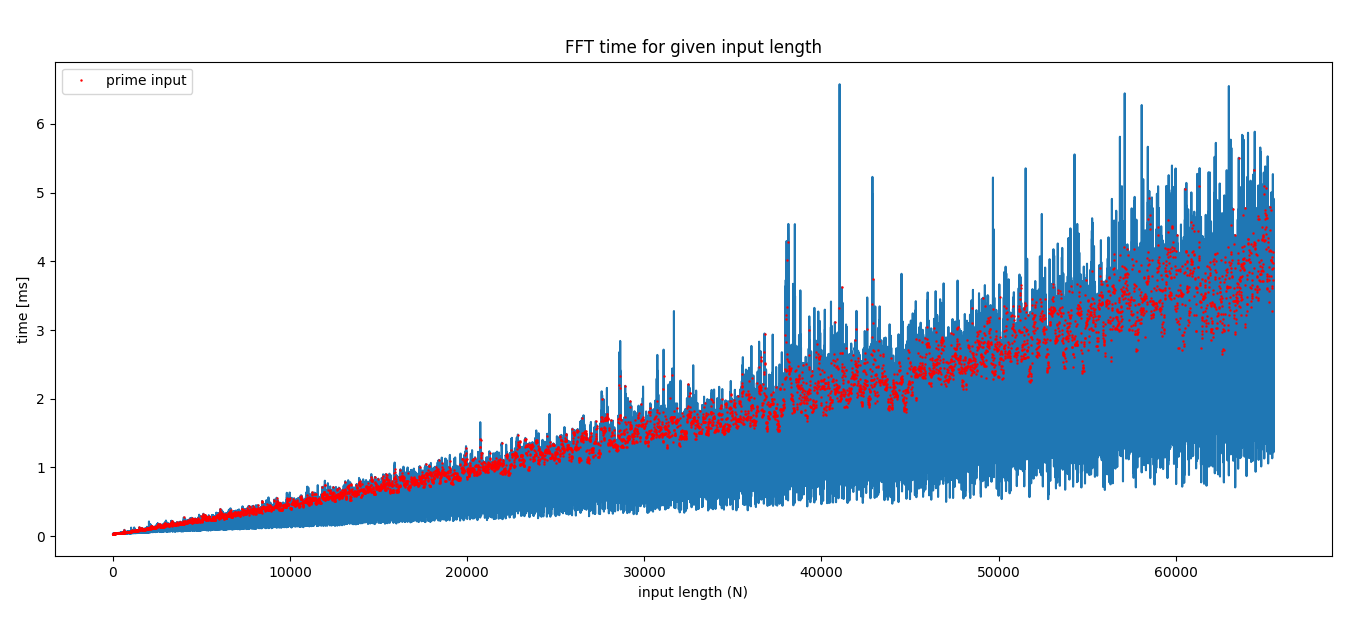
My takeaways here are:
- FFT of primes is definitely slower, up to ~5x (eyeballing it from the graph)
- Still, FFT is generally very fast even for large inputs
- Remember padding the input to avoid primes will also take some time (and memory) and may introduce window artifacts (though not padding doesn't guarantee absence of artifacts)
- As always, benchmark your specific application to see if this is meaningful (e.g. if you're doing an N-D FFT or calling it in a tight loop)